Thông tin liên hệ
- 036.686.3943
- admin@nguoicodonvn2008.info

Căn bậc 2 trong Python có thể viết theo cách cực kỳ dễ dàng. Dưới đây là cách viết chương trình căn trong Python.
Python là một trong số ngôn ngữ lập trình phổ biến nhất hiện nay. Bạn dễ dàng tìm thấy nó xuất hiện ở những chương trình, phần mềm, web, khoa học dữ liệu, thậm chí cả học máy phổ biến hiện nay. Sở dĩ Python được ưa chuộng bởi nó hoạt động, lại dễ học và có thể chạy trên nhiều nền tảng khác nhau. Người dùng có thể tải Python miễn phí trên web chính thức của nhà phát hành, rồi tích hợp nó với các hệ thống thông dụng.
Khi học Python, bạn phải nắm được các hàm cơ bản, trong đó có tính căn bậc 2 Python.
Python có hàm sqrt() được xác định trước, trả về căn bậc hai của một số. Về cơ bản, nó tính căn bậc 2 trong Python. Hàm này xác định căn bậc 2 của một giá trị nhân chính nó để cho một số. Hàm sqrt() không được sử dụng trực tiếp để tìm căn bậc hai của một số đã cho, vì vậy chúng ta cần sử dụng mô-đun toán học - math để gọi hàm sqrt() trong Python.
Đề bài: Cho một số, hãy viết chương trình để tìm ra căn bậc hai của số đó.
Ví dụ:
Input: 25
Output: 5
Trong bài viết này, Quản Trị Mạng sẽ cùng các bạn tìm hiểu kỹ về căn bậc hai và cách viết chương trình tính căn bậc hai bằng ngôn ngữ lập trình Python.
Trong đại số học, bình phương của một số là kết quả của việc số đó nhân với chính nó: x = n*n, trong đó n*n = n2.
Bạn có thể tính bình phương trong Python như sau:
>>> n = 5 >>> x = n ** 2 >>> x 25
Toán tử ** trong Python được sử dụng để tính bình phương của một số. Trong trường hợp này, 5 bình phương hoặc 5 ngũ 2 bằng 25.
Khi đó, căn bậc hai là số n mà khi nhân với chính nó sẽ ra được bình phương x. Trong ví dụ này, căn bậc hai chính là 5.
25 là một bình phương hoàn hảo. Bình phương hoàn hảo là bình phương của các giá trị nguyên.
Ví dụ về bình phương hoàn hảo:
>>> 1 ** 1 1 >>> 2 ** 2 4 >>> 3 ** 3 9
Bạn có thể đã ghi nhớ những bình phương hoàn hảo này khi bạn học bảng cửu chương. Nếu bạn được cho một bình phương hoàn hảo với giá trị nhỏ, bạn có thể dễ dàng tính toán hoặc ghi nhớ căn bậc hai của nó. Tuy nhiên, đối với các bình phương khác, phép tính này có thể phức tạp hơn một chút.
Nhưng với tư cách một lập trình viên, bạn có thể tự tạo ra một công cụ tính căn bậc hai của riêng mình.
Mô-đun toán học của Python, một thư viện tiêu chuẩn, có thể giúp bạn giải quyết các vấn đề toán học trong khi code. Nó có chứa rất nhiều hàm hữu ích như remainder() và factorial(). Nó cũng có một hàm dành riêng cho việc tính căn bậc hai đó là sqrt().
Bạn sẽ bắt đầu bằng cách khai báo mô-đun toán học:
>>> import math
Mây giờ, bạn đã có thể sử dụng hàm math.sqrt() để tính toán căn bậc hai của một số.
sqrt() có một giao diện khá trực diện. Nó chỉ nhận có một tham số là x, như bạn thấy trong các ví dụ ở trên, x là đại diện cho bình phương bạn đang muốn tìm căn bậc hai.
Giá trị trả về của sqrt() là căn bậc hai của x, dưới dạng dấu phảy động. Nếu x = 25 như trong ví dụ trên thì kết quả trả về sẽ là 5.0.
Chúng ta sẽ xem xét một số ví dụ cụ thể và các cách tìm căn bậc hai của một số có sử dụng sqrt() và không sử dụng sqrt().
Số dương là loại đối số mà bạn có thể đưa vào hàm sqrt(), bao gồm cả kiểu int và float.
Ví dụ: Bạn có thể tính được căn bậc hai của 49 bằng cách sử dụng hàm sqrt() một cách đơn giản như sau (nhớ khai báo mô-đun math trước):
>>> math.sqrt(49) 7.0
Kết quả trả về sẽ là 7.0 dưới dạng số dấu phảy động.
Bên cạnh số nguyên, bạn cũng có thể đưa vào hàm sqrt() các giá trị kiểu float:
>>> math.sqrt(70.5) 8.396427811873332
Bạn có thể kiểm tra độ chính xác của phép tính căn bậc hai bằng cách thực hiện phép tính bình phương:
>>> 8.396427811873332 ** 2 70.5
Ngay cả số 0 cũng có thể được đưa vào hàm tính căn bậc hai của Python:
>>> math.sqrt(0) 0.0
Mặc dù bạn không cần phải tính căn bậc hai của số 0 bởi bạn thừa biết kết quả nhưng chúng ta vẫn cần phải nhắc tới bởi nếu không sẽ có lúc bạn đưa một biến vào hàm sqrt() mà giá trị của nó bạn không thực sự biết.
Bình phương của mọi số thực không thể âm. Kết quả của một phép nhân giữa hai số chỉ có thể âm nếu một số âm nhân với một số dương. Theo định nghĩa, bình phương của một số là kết quả của phép nhân nó với chính nó đo đó không thể có một số bình phương âm.
>>> math.sqrt(-25) Traceback (most recent call last): File "<stdin>", line 1, in <module> ValueError: math domain error
Nếu bạn cố đưa vào hàm sqrt() một số âm, bạn sẽ nhận được thông báo lỗi ValueError bởi vì hàm này không được lập trình để tính căn bậc hai của số âm. Do vậy, để tính căn bậc hai của số âm cần có một thuật toán phức tạp hơn, nằm ngoài phạm vi của hàm tính căn bậc hai của Python.
Trên thực tế, khi tham gia các buổi phỏng vấn vị trí lập trình viên Python, bạn có thể nhận được yêu cầu viết chương trình tính căn bậc hai của một số nhưng không được phép sử dụng các hàm có sẵn của Python. Do vậy, lúc này bạn sẽ phải tự xây dựng một thuật toán riêng để giải quyết vấn đề này.
Dưới đây là code mẫu của trường hợp này để các bạn tham khảo:
def mySqrt(x):
left = 1
right = x
mid = 0
while (left <= right):
mid = (left + right) // 2
if mid * mid == x:
return mid
elif mid * mid > x:
right = mid - 1
else:
left = mid + 1
sqrt = mid
return sqrt
print(mySqrt(25))
Để thấy ứng dụng của một công cụ tính căn bậc hai trong đời thực, chúng ta sẽ xét ví dụ sau:
Hãy tưởng tượng rằng Rafael Nadal, một trong những vận động viên quần vợt nhanh nhất trên thế giới, vừa đánh một cú thuận tay ở góc sau, nơi đường cuối sân tiếp xúc với đường biên của sân quần vợt.

Bây giờ, giả sử đối thủ của Nadal đánh trả lại bằng một cú lên lưới sang góc đối diện, góc đường biên bên kia tiếp xúc với chân cột lưới.
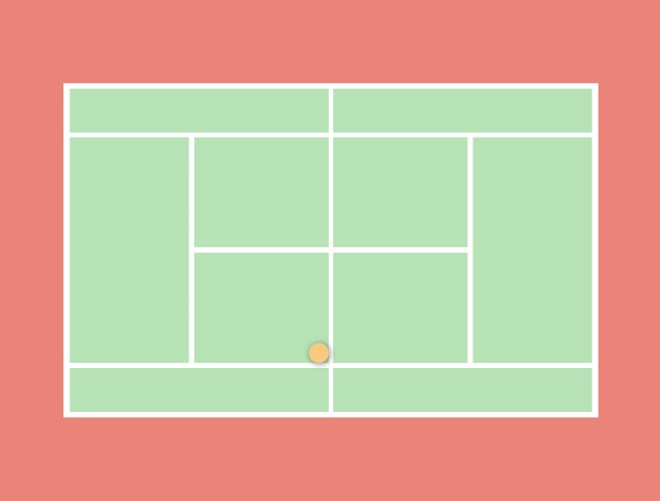
Naldal phải chạy bao xa để có thể đỡ được quả bóng?
Bạn có thể tính toán dựa trên kích thước quy định của sân quần vợt với đường cuối sân dài 27 feet (8,23 mét) và đường biên (một nửa sân) dài 39 feet (11,88 mét). Do đó, về cơ bản đây là bài toán tìm độ dài cạnh huyền của một tam giác vuông.
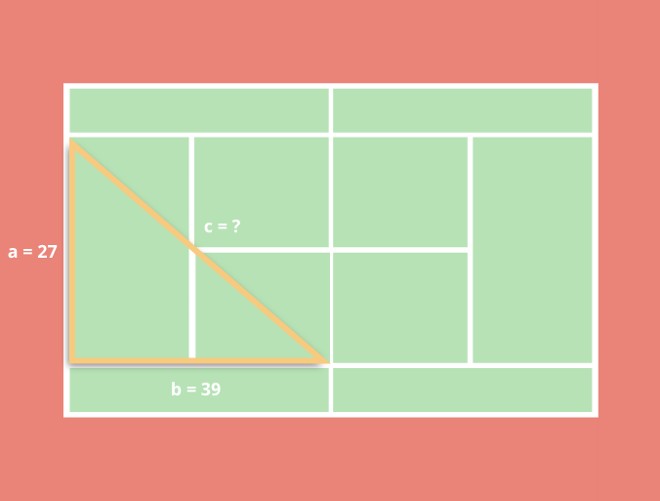
Chúng ta biết rằng với một tam giác vuông a² + b² = c². Do vậy, chúng ta có thể sắp xếp lại phương trình để tìm c:
Bây giờ, chúng ta có thể giải phương trình này bằng hàm tính căn bậc hai của Python:
>>> a = 27 >>> b = 39 >>> math.sqrt(a ** 2 + b ** 2) 47.43416490252569
Từ đó, kết quả trả về là Nadal phải chạy khoảng 47,4 feet (14,5 mét) để có thể tiếp cận trái bóng và giữ điểm.
Quản Trị Mạng hy vọng rằng bài viết này sẽ có ích đối với các bạn.
Nguồn tin: Quantrimang.com
Ý kiến bạn đọc
Những tin mới hơn
Những tin cũ hơn
 Cách sử dụng Samsung Internet trên PC Windows
Cách sử dụng Samsung Internet trên PC Windows
 Microsoft chặn luôn “chiêu” kích hoạt “lậu” Windows 10/11 phổ biến
Microsoft chặn luôn “chiêu” kích hoạt “lậu” Windows 10/11 phổ biến
 Thẻ chú thích trong HTML
Thẻ chú thích trong HTML
 Hướng dẫn sử dụng Microsoft PC Manager để nâng cao năng suất trên Windows
Hướng dẫn sử dụng Microsoft PC Manager để nâng cao năng suất trên Windows
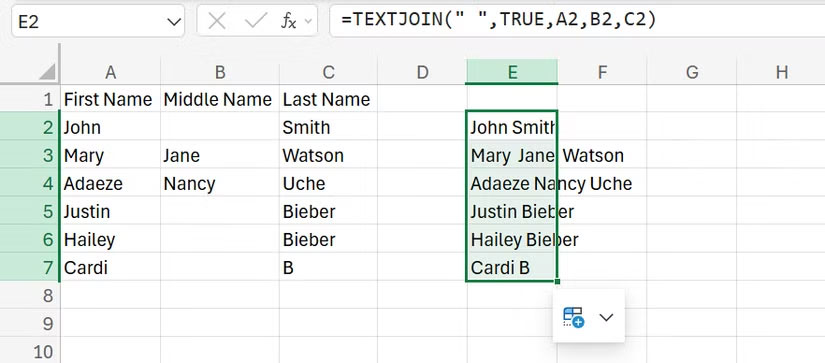 5 hàm giúp dọn dẹp ngay lập tức bảng tính Excel lộn xộn
5 hàm giúp dọn dẹp ngay lập tức bảng tính Excel lộn xộn
 Tại sao nên chuyển từ Chrome sang Cromite để giúp PC chạy nhanh hơn?
Tại sao nên chuyển từ Chrome sang Cromite để giúp PC chạy nhanh hơn?
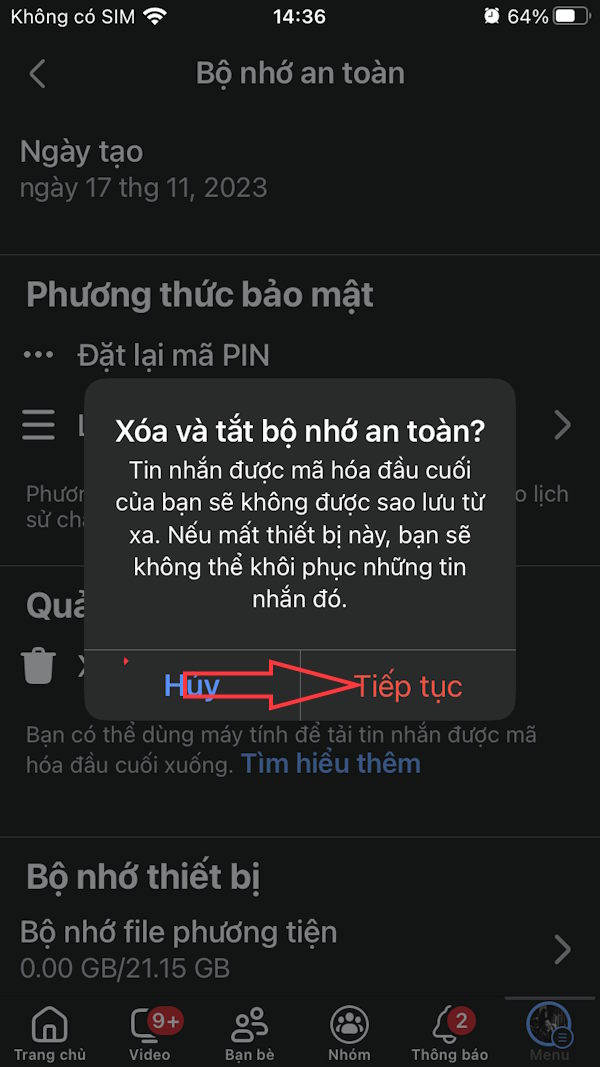 Cách tắt mã hóa đầu cuối trên Messenger
Cách tắt mã hóa đầu cuối trên Messenger
 Hai mặt của tình mẫu tử trong “Phá Đám: Sinh Nhật Mẹ”
Hai mặt của tình mẫu tử trong “Phá Đám: Sinh Nhật Mẹ”
 Bình dị hoa sen
Bình dị hoa sen
 Kí tự chữ nhỏ, ký tự số nhỏ FF
Kí tự chữ nhỏ, ký tự số nhỏ FF
 Cách mở và sử dụng Windows Terminal ở chế độ Quake Mode
Cách mở và sử dụng Windows Terminal ở chế độ Quake Mode
 Lấy lại Windows Photo Viewer trên Windows 10 giúp xem ảnh nhanh hơn, Photos chậm quá!
Lấy lại Windows Photo Viewer trên Windows 10 giúp xem ảnh nhanh hơn, Photos chậm quá!
 5 công cụ Windows nguồn mở vượt trội hơn hẳn so với đối thủ cạnh tranh
5 công cụ Windows nguồn mở vượt trội hơn hẳn so với đối thủ cạnh tranh
 Những công cụ thay đổi quan điểm người dùng về tính đa nhiệm của Linux
Những công cụ thay đổi quan điểm người dùng về tính đa nhiệm của Linux
 Cách truy cập điện thoại Android từ File Explorer Windows 11
Cách truy cập điện thoại Android từ File Explorer Windows 11
 Cách bật tính năng duyệt web an toàn nâng cao ‘Enhanced Safe Browsing’ trên Google Chrome
Cách bật tính năng duyệt web an toàn nâng cao ‘Enhanced Safe Browsing’ trên Google Chrome
 Đã có thể chuyển tệp và thư mục từ Dropbox sang Google Drive
Đã có thể chuyển tệp và thư mục từ Dropbox sang Google Drive
 11 cách mở Recycle Bin trên Windows
11 cách mở Recycle Bin trên Windows
 Cách download Windows 10, tải file ISO Windows 10 từ Microsoft
Cách download Windows 10, tải file ISO Windows 10 từ Microsoft
 Xóa tận gốc các file "cứng đầu" nhất trên Windows
Xóa tận gốc các file "cứng đầu" nhất trên Windows
